3 Top Blog Entries Over the Last 7 Days

A Peek into Einstein's Zurich Notebook
- By John D. Norton
- |
- Feb 21, 2019
Kudos to Professor John D. Norton at the Department of History and Philosophy of Science at the University of Pittsburgh for sharing and codifying Einstein's Zurich notebook. Here we see Einstein recounting the elements of the four-dimensional approach to relativity and electrodynamics of Minkowski, starting with the four spacetime coordinates (x, y, z, ict) = (x1, x2, x3, x4) and proceeding through scalars, four-vectors and six-vectors and the operations allowed with them. See more here.
John Morgan's beautiful brain on Riemannian Covariance Matrices
- By Rory Lewis
- |
- Feb 3, 2019
John W. Morgan | Lecture 1 | Introduction to Riemannian geometry, curvature and Ricci flow. Absolutely fantastic lecture by the great John Morgan. John Morgan is a professor of mathematics and founding director of the Simons Center for Geometry and Physics at Stony Brook University. His work is in the areas of geometry and topology. He has concentrated study of manifolds and smooth algebraic varieties. His most recent works include books, jointly with Gang Tian, explaining in detail the proof of the Poincaré conjecture and the geometrization conjecture, both of which concern the nature of three-dimensional spaces. See here.

Raymond Smullyan, Puzzle-Creating Logician, Dies at 97
- By Richard Sandomir, NYT
- |
- Posted Oct 2020 / 2017 article
Raymond Smullyan, whose merry, agile mind led him to be a musician, a magician, a mathematician and, most cunningly, a puzzle-creating logician, died on Monday in Hudson, N.Y. He was 97. His death was confirmed by Deborah Smullyan, a cousin. Professor Smullyan was a serious mathematician, with the publications and the doctorate to prove it. But his greatest legacy may be the devilishly clever logic puzzles that he devised, presenting them in numerous books or just in casual conversation. See here.
Blog Entries Over Time

Abel Laureate Interview
- By John Tate, Abel Laureate Interview (2010)
- |
- Dec 20, 2020
“... One big difference in mathematics generally is the advent of high-speed computers. Even for pure math, that will increase the experimental possibilities enormously. It has been said that number theory is an experimental science, and until recently that meant experimenting by looking at examples by hand and discovering patterns that way. Now we have a zillionfold more powerful way to do that, which may very well lead to new ideas even in pure math, but certainly also for applications. Mathematics somehow swings between the development of new abstract theories and the application of these to more concrete problems and from concrete problems to theories needed to solve them. The pendulum swings. When I was young better foundations were being developed, things were becoming more functorial, if you will, and a very abstract point of view led to much progress. But then the pendulum swung the other way to more concrete things in the 1970s and 1980s. There were modular forms and the Langlands program, the proof of the Mordell conjecture and of Fermat’s last theorem. In the first half of my career, theoretical physics and mathematics were not so close. There was the time when the development of mathematics went in the abstract direction, and the physicists were stuck. But now in the last thirty years they have come together. It is hard to tell whether string theory is math or physics. And noncommutative geometry has both sides. Who knows what the future will be? I don’t think I can contribute much in answering that question. Maybe a younger person would have a better idea.” -John Tate, Abel Laureate Interview (2010)

Feynman's Lost Lecture (ft. 3Blue1Brown)
- By minutephysics Created by Henry Reich
- |
- Dec 20, 2020
This video recounts a lecture by Richard Feynman giving an elementary demonstration of why planets orbit in ellipses. See the excellent book by Judith and David Goodstein, "Feynman's lost lecture”, for the full story behind this lecture, and a deeper dive into its content. Tweet referenced at the start: https://twitter.com/3blue1brown/statu... Music by Nathaniel Schroeder: https://soundcloud.com/drschroeder/el... Music by Vincent Rubinetti: https://soundcloud.com/vincerubinetti... Support MinutePhysics on Patreon! http://www.patreon.com/minutephysics Link to Patreon Supporters: http://www.minutephysics.com/supporters/ MinutePhysics is on twitter - @minutephysics And facebook - http://facebook.com/minutephysics And Google+ (does anyone use this any more?) - http://bit.ly/qzEwc6 Minute Physics provides an energetic and entertaining view of old and new problems in physics -- all in a minute!

Richard Feynman, Murray Gell-Mann and others
- By California Institute of Technology
- |
- Dec 20, 2020
“Pauli’s whole character was different from mine. He was much more critical, and he tried to do two things at once. I, on the other hand, generally thought that this is really too difficult, even for the best physicist. He tried, first of all, to find inspiration in the experiments and to see, in a kind of intuitive way, how things are connected. At the same time, he tried to rationalize his intuitions and to find a rigorous mathematical scheme, so that he really could prove everything he asserted. Now that is, I think, just too much. Therefore Pauli has, through his whole life, published much less than he could have done if he had abandoned one of these two postulates. Bohr had dared to publish ideas that later turned out to be right, even though he couldn’t prove them at the time. Others have done a lot by rational methods and good mathematics. But the two things together, I think, are too much for one man.” -Werner Heisenberg (describing Wolfgang Pauli’s approach to physics).

Heisenberg describing Pauli
- By IAEA Bulletin special supplement (1968), p. 45.
- |
- Dec 20, 2020
“Pauli’s whole character was different from mine. He was much more critical, and he tried to do two things at once. I, on the other hand, generally thought that this is really too difficult, even for the best physicist. He tried, first of all, to find inspiration in the experiments and to see, in a kind of intuitive way, how things are connected. At the same time, he tried to rationalize his intuitions and to find a rigorous mathematical scheme, so that he really could prove everything he asserted. Now that is, I think, just too much. Therefore Pauli has, through his whole life, published much less than he could have done if he had abandoned one of these two postulates. Bohr had dared to publish ideas that later turned out to be right, even though he couldn’t prove them at the time. Others have done a lot by rational methods and good mathematics. But the two things together, I think, are too much for one man.” -Werner Heisenberg (describing Wolfgang Pauli’s approach to physics).

Theoretician Mary Gaillard and Murray Gell-Mann at CERN (1972)
- By Rory Lewis
- |
- June 24, 2020
Madame Gaillard et Monsieur Gell-Mann distant devant un tableau noir The Theory Division welcomed Nobel Prize Winner Murray Gell-Mann for a stay. He is here in discussion with Mary Gaillard. All of modern physics is governed by that magnificent and thoroughly confusing discipline called quantum mechanics ... It has survived all tests and there is no reason to believe that there is any flaw in it. We all know how to use it and how to apply it to problems; and so we have learned to live with the fact that nobody can understand it.” -Murray Gell-Mann
A Machine Consciousness architecture based on Deep Learning and Gaussian Processes
- By Merchán et. al
- |
- April 23, 2020
Kudos to Eduardo Merchán and Martín Molina for a novel way of invoking consciousness in machines with an architecture based in processes that use the recent developments in artificial intelligence models which output are these correlated activities. For every one of the modules of this architecture, they provide detailed explanations of the models involved and how they communicate with each other to create the cognitive architecture.Merchán, Eduardo C. Garrido, and Martín Molina. "A Machine Consciousness architecture based on Deep Learning and Gaussian Processes." arXiv preprint arXiv:2002.00509 (2020)..

1 year after epic black hole photo, Event Horizon Telescope team is dreaming very big
- By Mike Wall, space.com
- |
- April 19, 2020
The Event Horizon Telescope, a planet-scale array of eight ground-based radio telescopes forged through international collaboration, captured this image of the supermassive black hole and its shadow that's in the center of the galaxy M87. In April 2019, the EHT collaboration revealed the first-ever image of a black hole, which captured the behemoth at the heart of the galaxy M87. The project had been working for that moment for two decades, but the unveiling did not mark a climax or a culmination. Rather, it was a turning point, the opening of a window onto even more exciting discoveries to come, team members said..

John Horton Conway, a ‘Magical Genius’ in Math, Dies of Corona Virus
- By Siobhan Roberts, NYT
- |
- April 17, 2020
John Horton Conway, the English-born Princeton mathematician whose body of work ranged from the rigorously highbrow to the frivolously fun, earning him prizes and a reputation as a creative, iconoclastic and even magical genius, died on Saturday in New Brunswick, N.J. He was 82. “His swath was probably broader than anyone who ever lived,” said the mathematician Neil Sloane, a collaborator with Dr. Conway and the founder of the On-Line Encyclopedia of Integer Sequences. “I’ve worked with a lot of people, and he was the fastest at solving a problem and would pursue a topic as far as it would go.”.
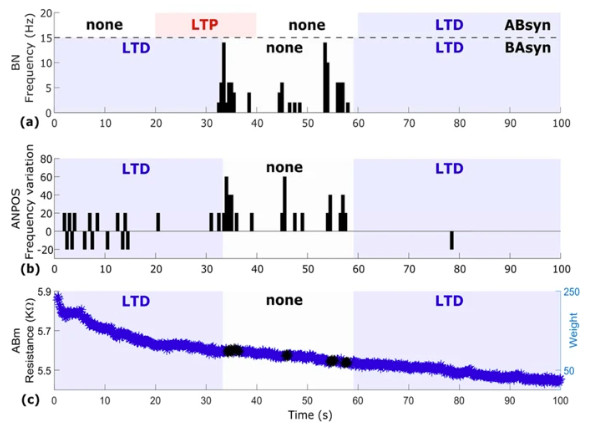
Linking Brain and Artifical Nerurons to the Web
- By Serb et. al
- |
- February 25, 2020
Kudos to Alexantrou Serb and his fellow researchers for using a memristor paired with a titanium oxide microelectrode and silicon neurons and the web. Using that, and demonstrating how memristive plasticity accounts for connection strength, replicating exitatory postsynapict potentials. Serb, A., Corna, A., George, R., Khiat, A., Rocchi, F., Reato, M., Maschietto, M., Mayr, C., Indiveri, G., Vassanelli, S., Prodromakis, T. 2020. Memristive synapses connect brain and silicon spiking neurons. Scientific Reports, 10 (1) DOI: 10.1038/s41598-020-58831-9.

Swarming robots avoid collisions
- By Rubenstein et. al
- |
- February 17, 2020
Kudos to Michael Rubenstein and Hanlin Wang on creating collsion-free pathing for robotic swarms. Using a distributed algorithm to move the robots in a formation to specify shapes and goal locations. This algorithm was executed on a swarm of up to 1024 simulated robots and 100 real robots reliably too. Rubenstein, M., Wang, H., 2020. Shape Formation in Homogeneous Swarms Using Local Task Swapping. IEEE Transactions on Robotics, 2020; 1 DOI: 10.1109/TRO.2020.2967656.
Fractional order neural networks for system identification
- By Kalamka et. al
- |
- September 22, 2019
Kudos to Dhiraj Kalamka and his fellow researchers at Intel where they efficacy of the Brain Floating Point (BFLOAT16) half-precision format for Deep Learning training across image classification, speech recognition, language modeling, generative networks and industrial recommendation systems. Kalamkar, D., Mudigere, D., Mellempudi, N., Das, D., Banerjee, K., Avancha, S., Vooturi, D.T., Jammalamadaka, N., Huang, J., Yuen, H. and Yang, J., 2019. A Study of BFLOAT16 for Deep Learning Training. arXiv preprint arXiv:1905.12322.
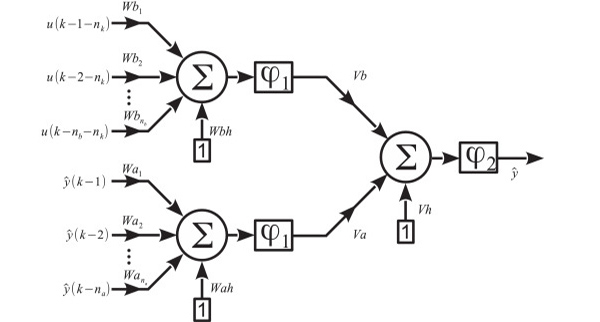
Fractional Order Neural Networks for System Identification
- By Aguilar et. al
- |
- September 19, 2019
Kudos to Aguilar et. al., fantastic paper on fractional order neural networks (FONN) for system identification where their learning algorithm was generalized considering the Grünwald-Letnikov fractional derivative. They validated their new black box modeling approach by the identification of three different systems (two benchmark systems and a real system). Comparisons vs others approaches showed that the proposed FONN model reached better accuracy with less number of parameters. Aguilar, C.Z., Gómez-Aguilar, J.F., Alvarado-Martínez, V.M. and Romero-Ugalde, H.M., 2020. Fractional order neural networks for system identification. Chaos, Solitons & Fractals, 130, p.109444.

Breakthrough for A.I. Technology: Passing an 8th-Grade Science Test
- By Cade Metz
- |
- September 8, 2019
Kudos to Drs. Oren Etzioni, left, & Peter Clark, managers of the Aristo project at the the Allen Institute for Artificial Intelligence. After many previous competitions by colleagues in the field of artificial intelligence, to create an AI system that could pass an 8th Grade Science Examination, the team have succeeded in creating an AI system that does indeed pass an 8th-Grade Science Test, and get 80% on a 12th grade Science examination. Read here.
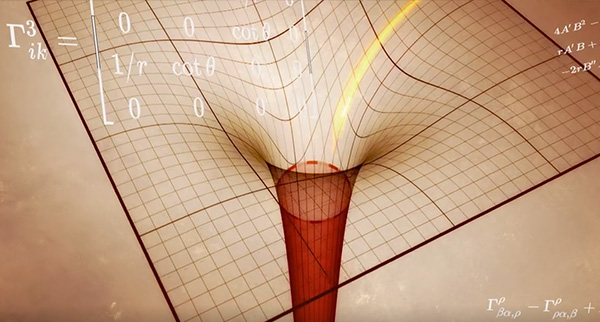
Black Hole Apocalypse
- By Nova
- |
- August 12, 2019
See Fantastic documentary of black holes and how Kip Thorne wagered with Paul Murdin as to whether black holes existed and how they proved it did. This is a fantastic documnetary. Start it at 4:15. Take a mind-blowing voyage to the most powerful and mysterious objects in the universe. Black holes are the most enigmatic and exotic objects in the universe. They’re also the most powerful, with gravity so strong it can trap light.

2018 Taulbee Survey: Data of US & Canada Computer Sciences 2018 Released
- By Zweben & Bizot
- |
- July 9, 2019
Undergrad Enrollment Continues Upward; Doctoral Degree Production Declines but Doctoral Enrollment Rises. The survey, conducted annually by the Computing Research Association, documents trends in student enrollment, degree production, employment of graduates, and faculty salaries in academic units in the United States and Canada that grant the Ph.D. in computer science (CS), computer engineering (CE), or information (I). Download here.

Murray Gell-Mann, Who Peered at Particles and Saw the Universe, Dies at 89
- By George Johnson
- |
- May 24, 2019
Dr. Murray Gell-Mann in 1953 or 1954. He collaborated with the renowned physicist Richard Feynman at Caltech. Much as atoms can be slotted into the rows and columns of the periodic table of the elements, Dr. Gell-Mann found a way, in 1961, to classify their smaller pieces — subatomic particles like protons, neutrons, and mesons, which were being discovered by the dozen in cosmic rays and particle accelerator blasts. Arranged according to their properties, the particles clustered in groups of eight and 10.
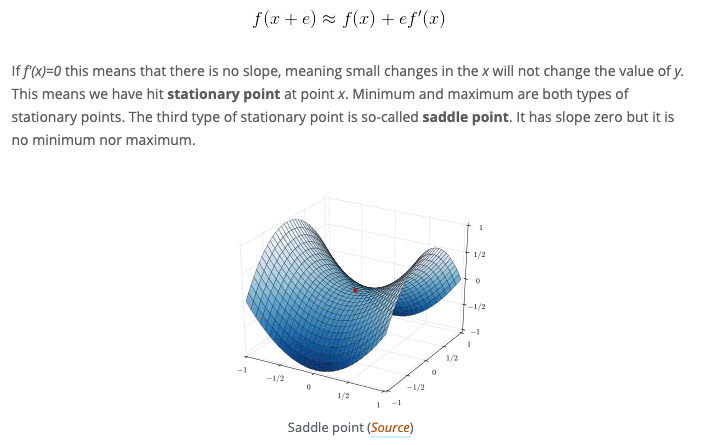
Mathematics for Artificial Intelligence – Calculus & Optimization
- By Nikola Živković, U. of Novi Sad
- |
- May 13, 2019
This is a very well laid out article, well written, that does a great job identifying and focusing on the essential elements in machine learning that are extrinsically linked to mathematical principles. Nikola Živković answers a questioni I often hear from students, "How much math should I know in order to get into the field?” -- In particular, "How much calculus do I need for artificial intelligence and machine learning?". Živković answers these questions by eloquently stating "Machine learning and deep learning applications usually deal with something that is called the cost function, objective function or loss function. "
See moore at his blog here.
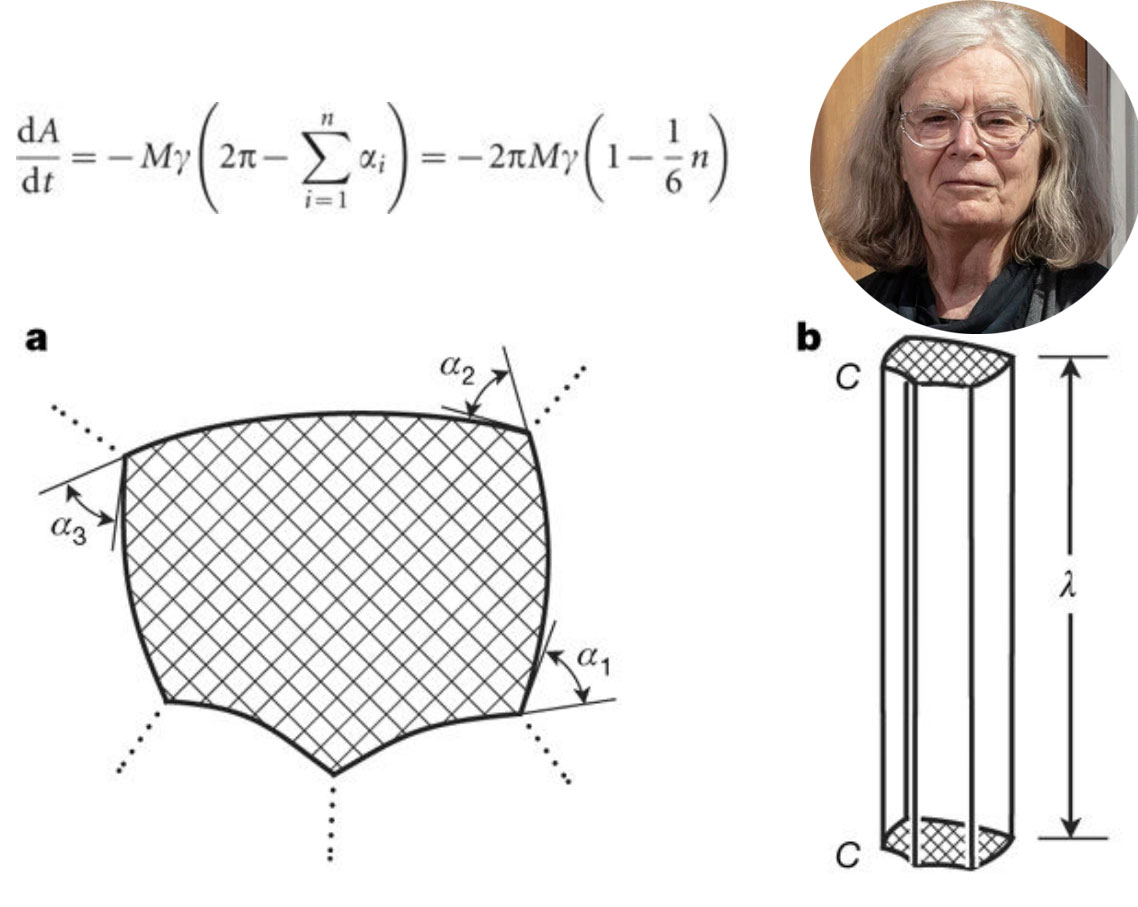
Congrats to Karen Uhlenbeck; first woman to win Abel Prize for mathematics
- By Siobhan Roberts. NYT
- |
- April 19, 2019
Dr. Uhlenbeck was awarded the Abel prize for her discovery of a phenomenon called “bubbling,” among other effervescent results. Even Robert MacPherson, a topologist and faculty member in mathematics at the institute, made a rare social appearance. A decade ago, Dr. MacPherson and a collaborator formulated an equation describing how, in three and higher dimensions, individual bubbles evolve in live foams — the fleeting foam at the meniscus in his champagne flute, for instance, or the more enduring head on a pint of beer. Dr. Uhlenbeck’s contribution is her pioneering achievements in geometric partial differential equations, gauge theory and integrable systems. Here dA/dt is the rate of change of the area of a domain, αi is the exterior (turning) angle at a triple junction on that domain (where three domain walls meet - looking at a.>.See journal paper here.

How the brain distinguishes between objects
- By Saxton, Grefenstette, Hill, Kohli
- |
- March 21, 2019
Now available on GitHub. This is the version released with the original paper. It contains 2 million (question, answer) pairs per module, with questions limited to 160 characters in length, and answers to 30 characters in length. Note the training data for each question type is split into "train-easy", "train-medium", and "train-hard". This allows training models via a curriculum.
See the original paper here
Download the data set and code from GitHub here

Good introductory video
- By Rory Lewis
- |
- April 2, 2019
Start watching Bill Shander's class on Skillshare
Mike Bostock, master "observer
- By Rory Lewis
- |
- April 2, 2019
Excerpt from Mike Bostock · Jun 15, 2018. See here. For example, say I’m happily biking along 🚲😅 at when I get passed by a car 🚗💨 going . I might think: Yikes! That car was going three times my speed! Or: That car was going faster than me! (Cars are scary!) Or maybe I’m a cryptocurrency speculator, and I bought one Dinglecoin at the start of the year for and then sold it yesterday for . I’d say: *Oops, my return was *. Maybe I should invest elsewhere. There are many ways to compare values. Depending on what you seek to understand, one method may be better than another. In this post, we’ll walk through some common methods and consider their uses. Side-by-Side Let’s start by looking separately at 1980 and 2014. Hover over any of the counties to see the underlying values.
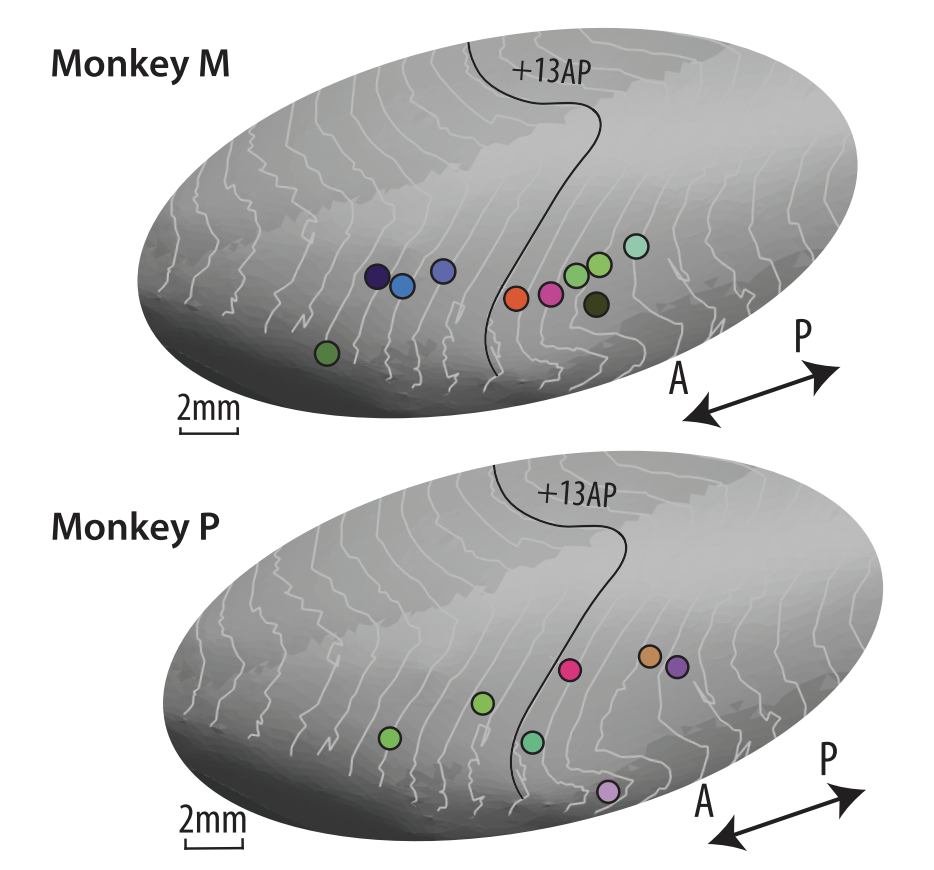
How the brain distinguishes between objects
- By Rory Lewis
- |
- March 21, 2019
Kudos to Professor James J. DiCarlo and Rishi Rajalingham1 for incredible work deciphering how the inferior temporal (IT) population supports visual object recognition behavior. In the image, for Experiment 1 (n = 10 in monkey M, n = 7 in monkey P) are shown; 8 other sites measured under Experiment 2 they observed spatial clustering of colors.They quantified the non-uniformity of the behavioral deficits using a sparsity index
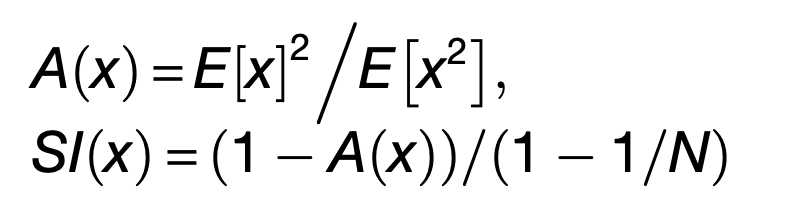
Rajalingham, Rishi, and James J. DiCarlo. "Reversible inactivation of different millimeter-scale regions of primate IT results in different patterns of core object recognition deficits." Neuron (2019).
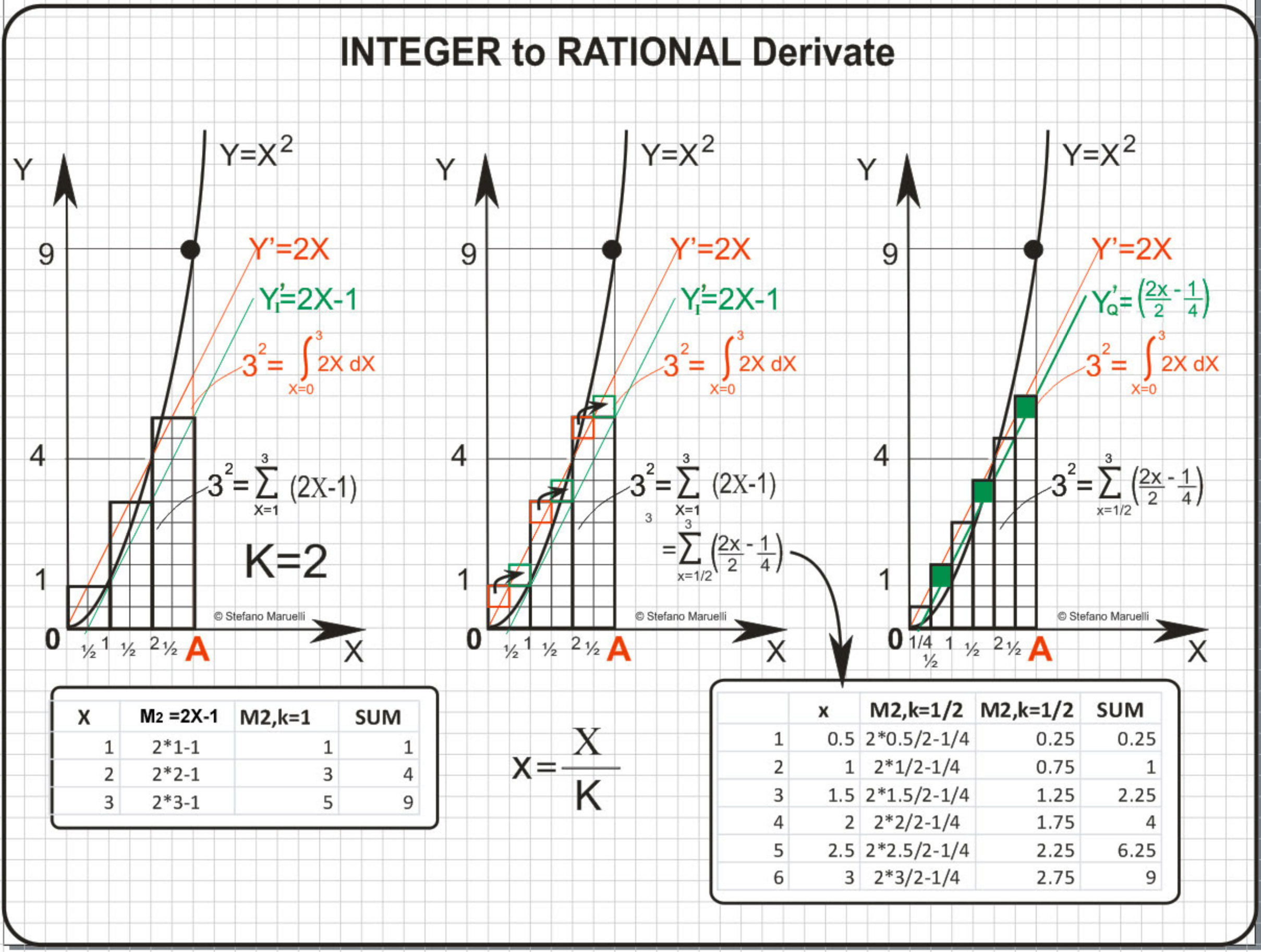
Integer to Rational Derivate
- By Stefano Maruelli
- |
- Feb 16, 2019
This image shows Here pushing the property to the limit (example in case n=3): Kudos to Stefano Maruelli on a very cool way make a Sum work its way into a Rational under certain conditions. The idea is to make a Sum capable to rise, for example, the Square of a Rational a=A/K. Of course n-th power representation of a Rational will follow by the same Telescoping Sum Property. Here is his example of a Step Sum capable to rise an Integer (A) and/or a Rational (A/K) Upper Limit, at the condition that Both the Upper and lower Limits are divisible by the Step (K) we choose.

For a Black Mathematician, What It’s Like to Be the ‘Only One’
- By New York Time's Amy Harmon
- |
- Feb 18, 2019
Fascinating article in NYT. Edray Goins frequently asked himself whether he was right to factor race into the challenges he faced: “Did it really happen that way, or am I blowing it out of proportion?” Photo. Jared Soares. Fewer than 1 percent of doctorates in math are awarded to African-Americans. Edray Goins, who earned one of them, found the upper reaches of the math world a challenging place. See full article in the New York Times here.
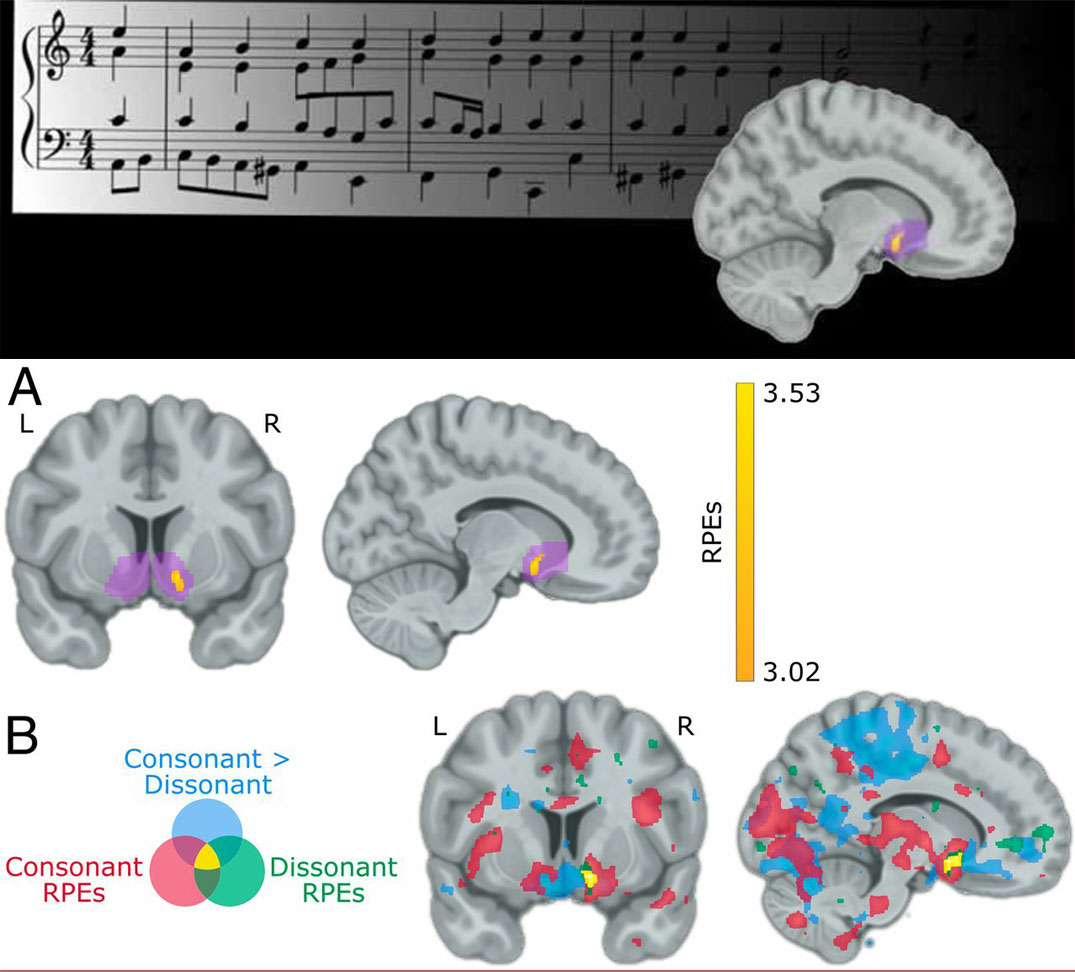
The Unexpected Creates Reward When Listening to Music
- By Neuroscience News Shawn Hayward
- |
- Feb 12, 2019
If you love it when a musician strikes that unexpected but perfect chord, you are not alone. New research shows the musically unexpected activates the reward centre of our brains, and makes us learn about the music as we listen. Researchers at McGill University put 20 volunteers through a musical reward learning task. Each participant chose a colour, then a direction. Continue @ Neuroscience News here or read the original paper here. Gold, Benjamin P., et al. Musical reward prediction errors engage the nucleus accumbens and motivate learning. Proceedings of the National Academy of Sciences Feb 2019.

Riemannian Covariance Matrices
- By Rory Lewis
- |
- Feb 6, 2019
Not that I am trying to draw in more than 3-Dimenions. But our hypothesis is that a manifold with n-dimenions with clustering could procure a machine learning system to learn different dimenions differently and thus become smart. Photo taken by Eli Brainard UCCS, Feb 6th, 2019. In general, one will find that Riemann distance is better for defining positive semidefinite matrices such as covariance matrices where one wants manifold to be able to retain n-dimenions, than Euclidian distance. To view equations, see larger version of photo here.
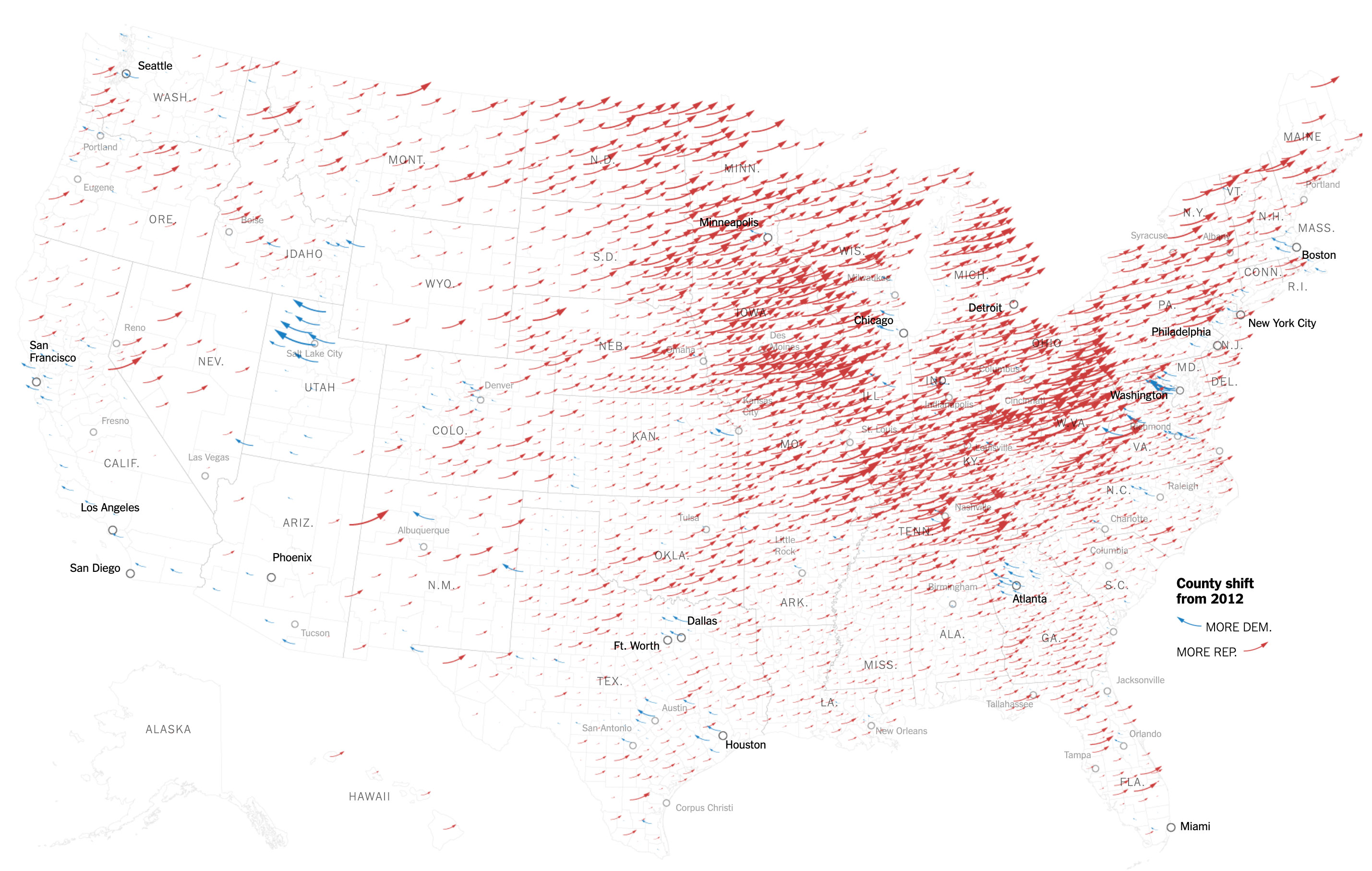
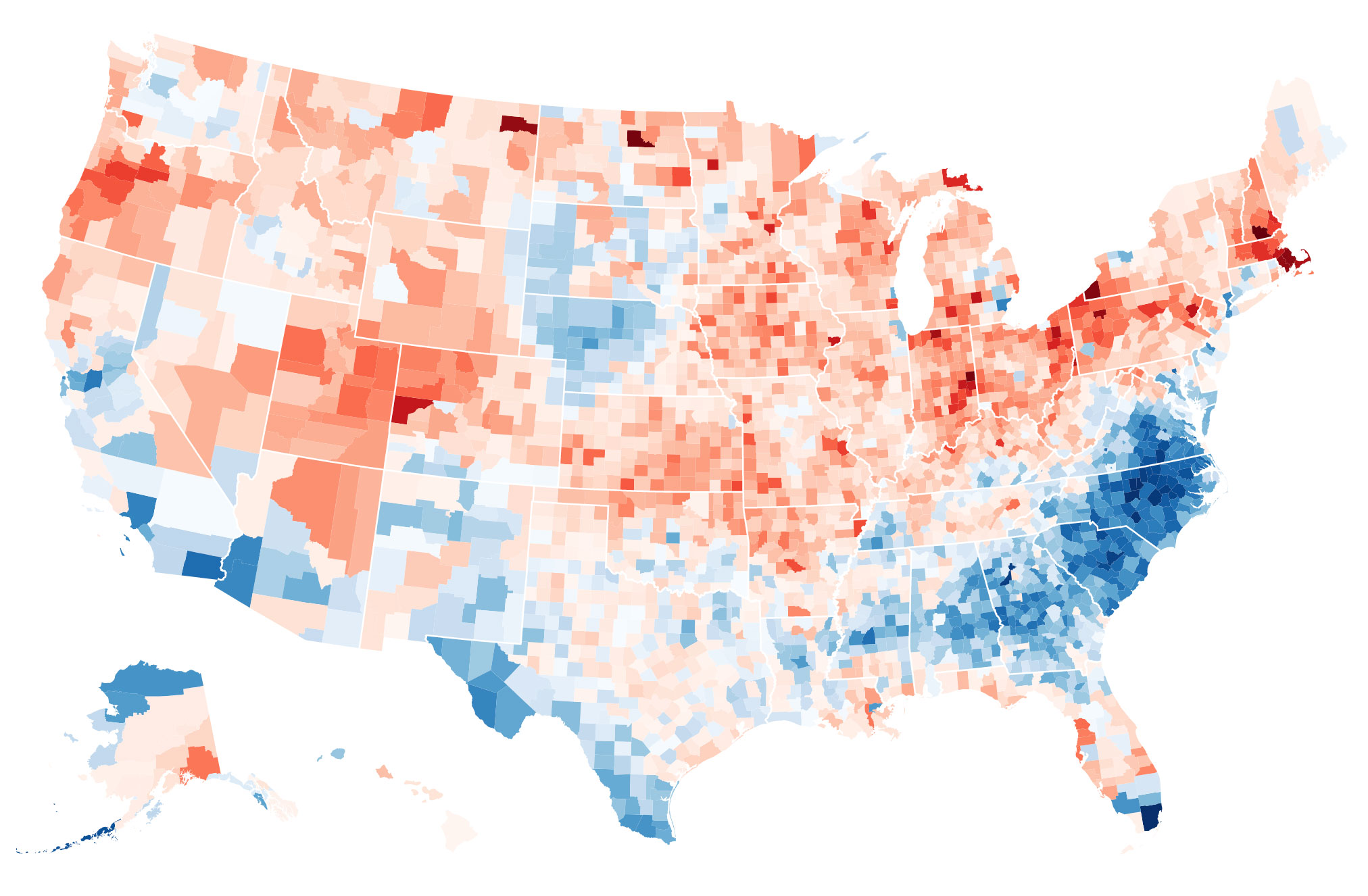
Political Engineering; How Trump's Artificial Intelligence Reshaped the Election Map
- By Rory Lewis
- |
- Dec 12, 2018
Bostok's amazing bigdata and very cool D3 award winning visualization. Specifically made to interact with artificial intelligence and graphics. This image shows the county shifts from 2012. See full article in the New York Times here.
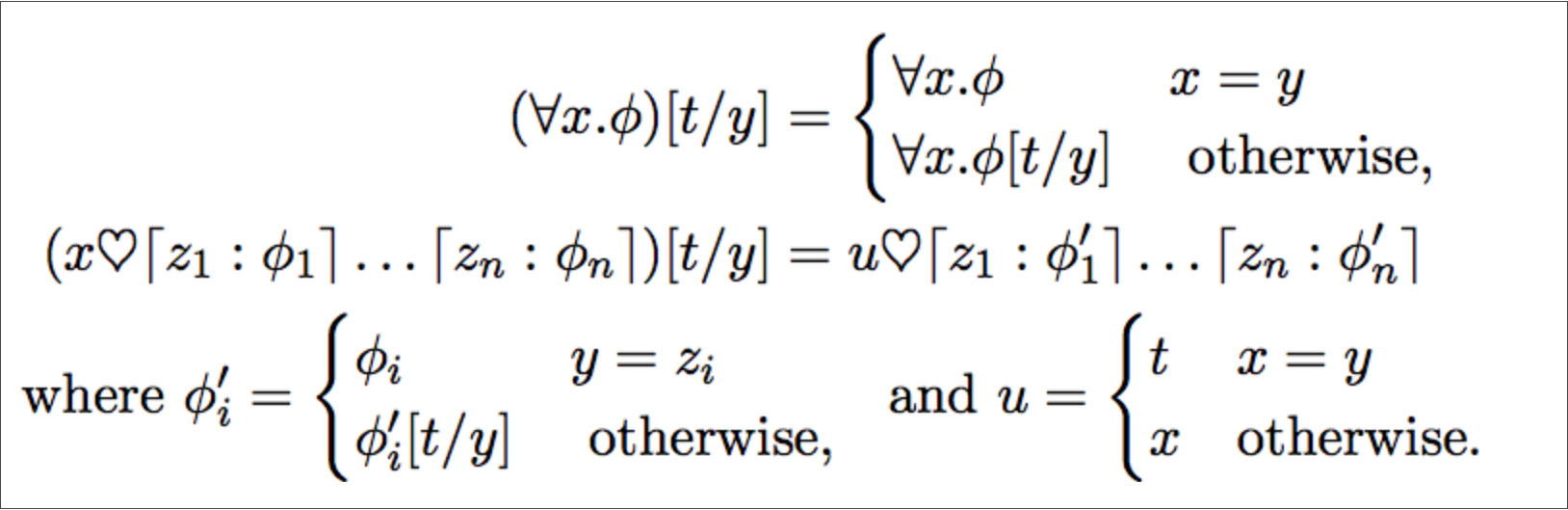
Model Theory and Proof Theory of Coalgebraic Predicate Logic
- By Tadeusz Litak
- |
- Mar 19, 2018
- |
- 06
Congrats to Tadeusz Litak et al. Generalization of first-order logic originating in a neglected work and show that an entirely general completeness result is NOT possible!
Abstract: We propose a generalization of first-order logic originating in a neglected work by C.C. Chang: a natural and generic correspondence language for any types of structures which can be recast as Set-coalgebras. We discuss axiomatization and completeness results for several natural classes of such logics. Continue reading here.
>Litak, Tadeusz, et al. "Model Theory and Proof Theory of Coalgebraic Predicate Logic." arXiv preprint arXiv:1701.03773 (2017).
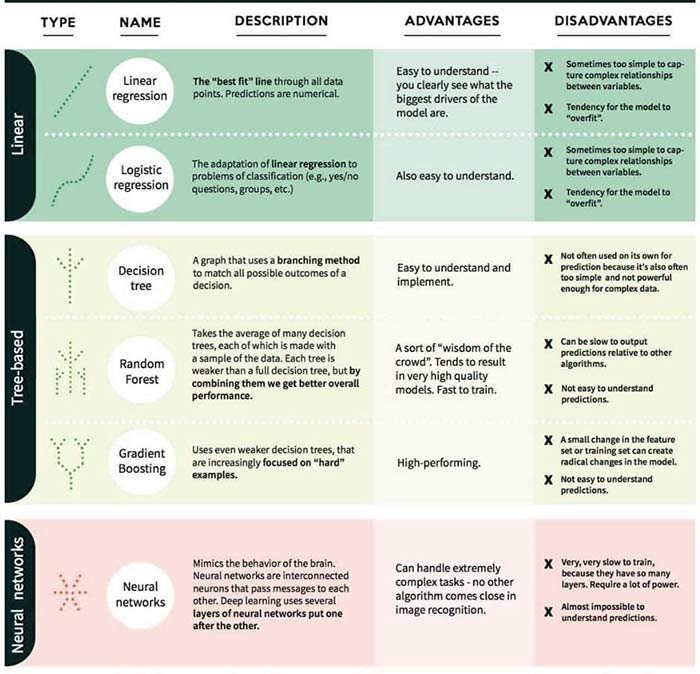
Classic Machine learning Algorithmse
- By Danny Varghese
- |
- Dec 06, 2018
Click on image, or here, to download a large readible version fo the image. Nice article by Danny Varghese overviewing some classic artificial intelligence adn machien learning algorithms. Machine learning is a scientific technique where the computers learn how to solve a problem, without explicitly program them. Deep learning is currently leading the ML race powered by better algorithms, computation power and large data. Still ML classical algorithms have their strong position in the field. See full article here.
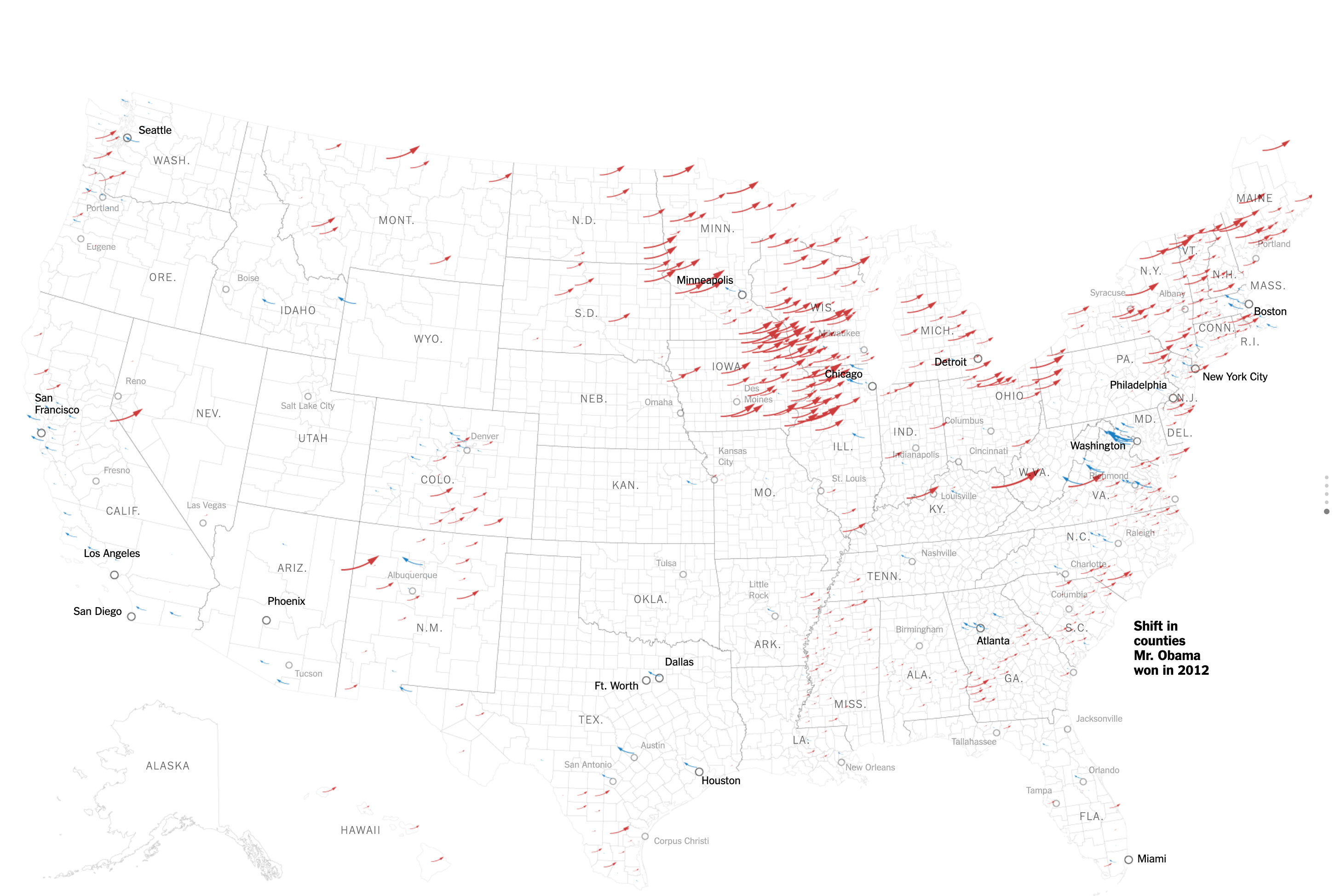
Political Engineering; How Trump's Artificial Intelligence Reshaped the Election Map
- By Rory Lewis
- |
- Dec 12, 2018
Bostok's amazing bigdata and very cool D3 award winning visualization. Specifically made to interact with artificial intelligence and graphics. This image shows the shift ijn counties Obama won in 2012.See full article in the New York Times here.

Putin Says the Nation That Leads in AI ’Will Be the Ruler of the World
- By James Vincent
- |
- Sep 4, 2017
The Russian president warned that artificial intelligence offers ‘colossal opportunities’ as well as dangers. Russian president Vladimir Putin has joined the war of words concerning the international race to develop artificial intelligence. Speaking to students last Friday, Putin predicted that whichever country leads the way in AI research will come to dominate global affairs. “Artificial intelligence is the future, not only for Russia, but for all humankind,” said Putin, reports RT. “It comes with colossal opportunities, but also threats that are difficult to predict. Whoever becomes the leader in this sphere will become the ruler of the world.”See full articlehere.
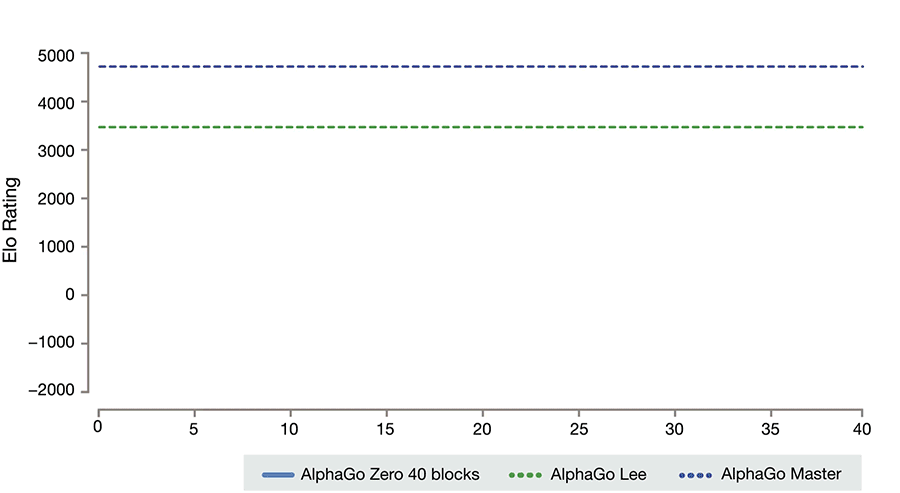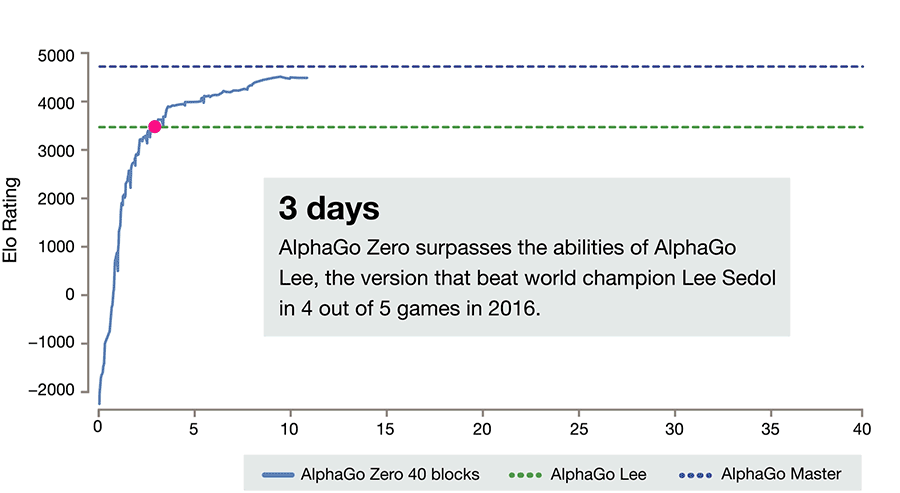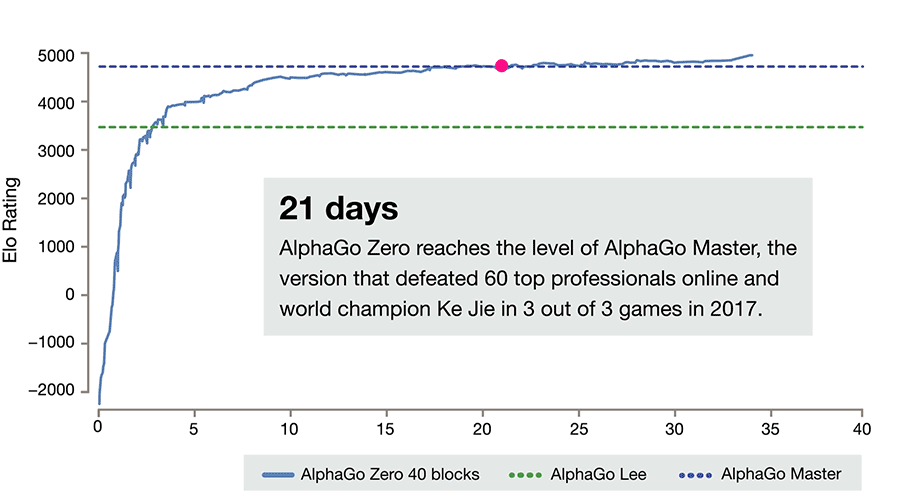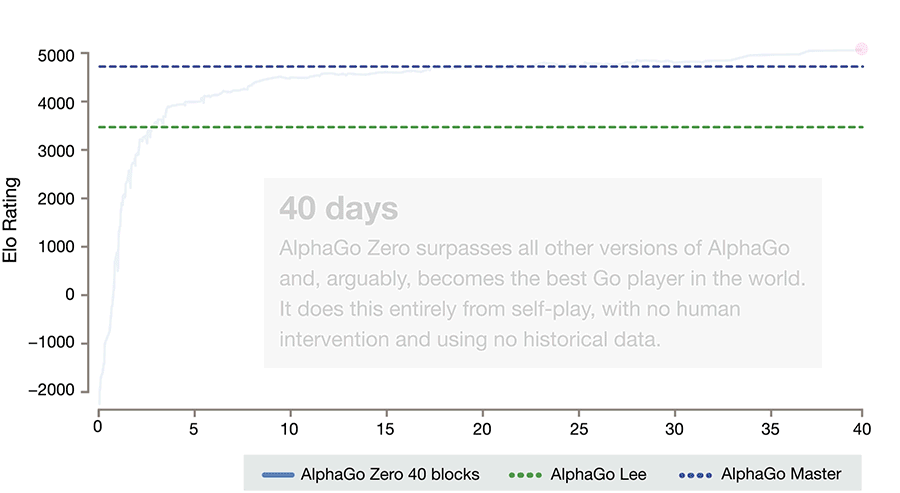
Deepmind’s Alphazero Beats The Top Ai Champions in Go, Shogi, and Chess
- By David Silver and Demis Hassabis
- |
- Oct 18, 2017
After just three days of self-play training, AlphaGo Zero emphatically defeated the previously published version of AlphaGo - which had itself defeated 18-time world champion Lee Sedol - by 100 games to 0. After 40 days of self training, AlphaGo Zero became even stronger, outperforming the version of AlphaGo known as “Master”, which has defeated the world's best players and world number one Ke Jie. See full article here.
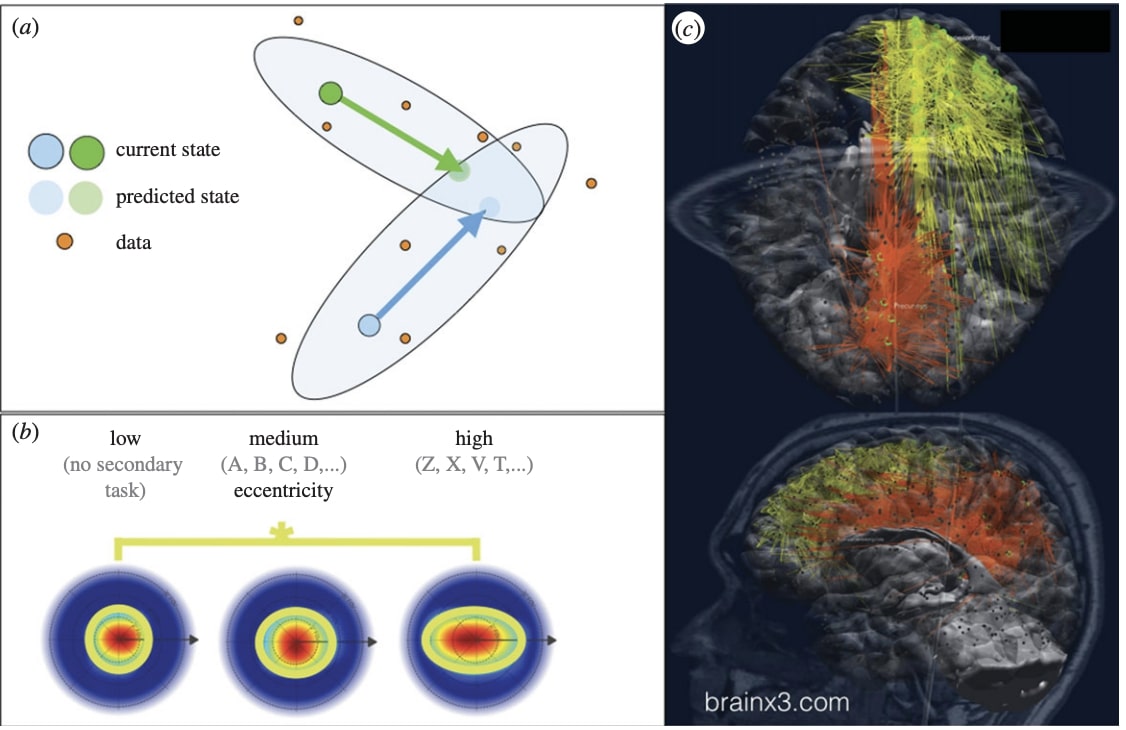
Synthetic Consciousness: the Distributed Adaptive Control Perspective
- By Paul Verschure,
- |
- May 18, 2016
Kudos to Paul Verschure at Laboratory of Synthetic Perceptive, Emotive and Cognitive Systems, Center of Autonomous Systems and Neurorobotics, Universitat Pompeu Fabra, Barcelona, Spain, for creating a functional hypothesis of synthetic consiousness that he mapped onto the brainstem, midbrain and the thalamo-cortical and cortico-cortical systems and analysed with respect to our understanding of deficits of consciousness. In teh image above form his paper, . Hemispatial neglect. (a) Standard drawing test performed by a patient (male, 64 years) with a right haemorrhagic stroke showing a reduced ability to fill the left side of a workspace with crosses. (b) A visual search task where subjects have to detect a local (top), global (middle) or combined (bottom) distractor in a visual display, which occurred with 50% probability in 72 trials. The distractors are indicated with a circle. The global distractor is a Kanizsa triangle. (c) Performance of control subjects and right hemispheric (RH) stroke patients in terms of accuracy (left column) and reaction time (RT; right column). For visibility, the RT of the control group is displayed in a reduced range, which is reflected with a dashed box in RT plots for RH. Asterisks indicates a significant difference at p , 0.01. Ncontrol: 10; NRH: 8 Verschure, Paul FMJ. "Synthetic consciousness: the distributed adaptive control perspective." Philosophical Transactions of the Royal Society B: Biological Sciences 371, no. 1701 (2016): 20150448. See full article here.
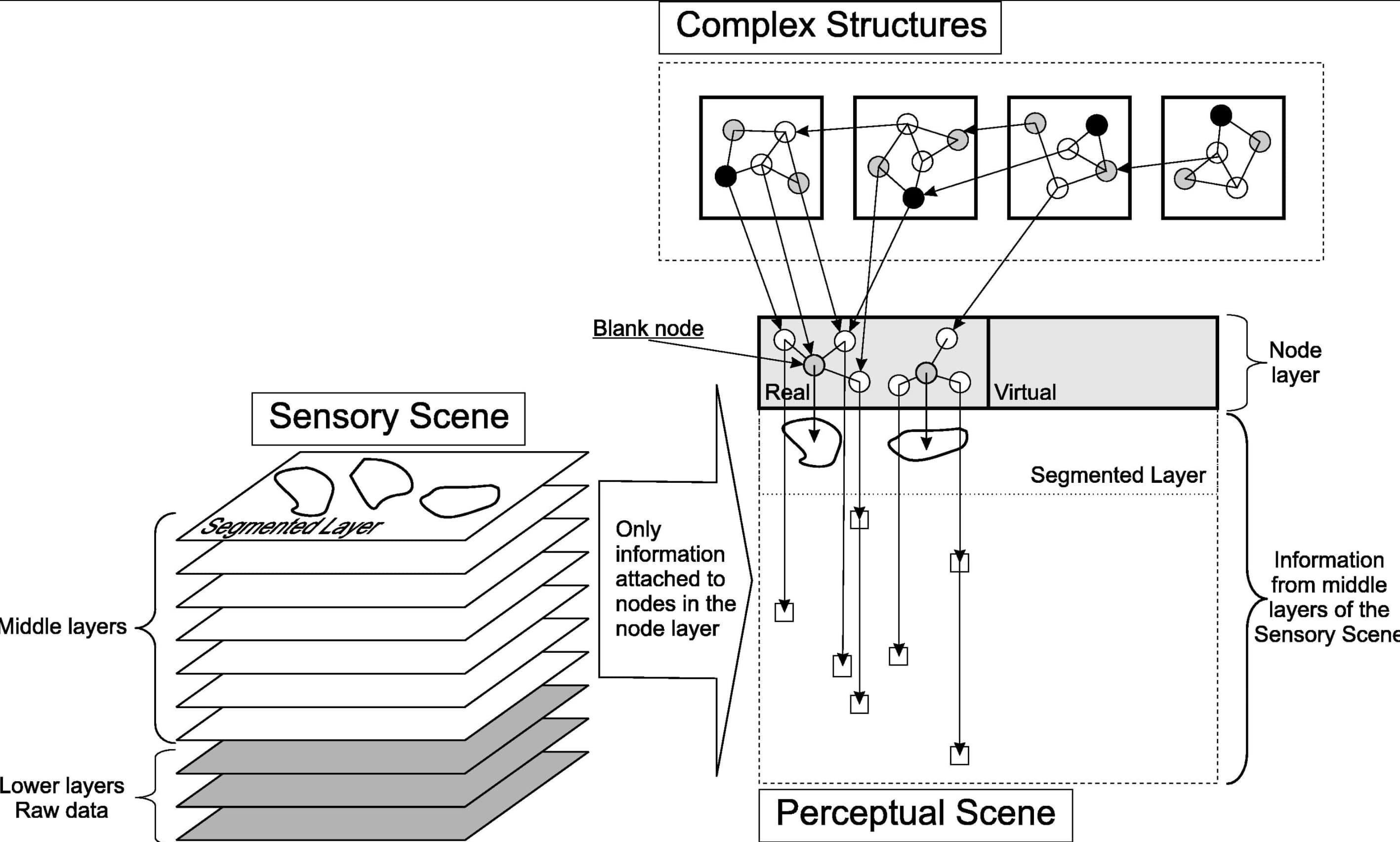
Synthetic Consciousness: the Distributed Adaptive Control Perspective
- By Stan Franklin, et al.
- |
- April 04, 2016
Kudos to Stan Franklin and his team at the University of Memphis for their tutorial of LIDA - their systems-level cognitive model. It is conceptual and partly computational. It attempts to model minds, be they human, animal or artificial, which he takes to be control structures for autonomous agents. They think of minds as being implemented as virtual machines running on top of underlying devices such as brains or computers. In addition to providing explanations and producing hypotheses, we aspire that LIDA act as a cognitive prosthesis to aid in thinking about, and understanding, individual cognitive activities and their processes. Franklin, Stan, Tamas Madl, Steve Strain, Usef Faghihi, Daqi Dong, Sean Kugele, Javier Snaider, Pulin Agrawal, and Sheng Chen. "A LIDA cognitive model tutorial." Biologically Inspired Cognitive Architectures 16 (2016): 105-130. See full article here.